専門分野
金融計量経済学、ファイナンス
研究テーマ
リスクマネジメント、予測
研究紹介
金融市場では、債券や株式など様々な資産が取引されています。そのような資産の価格や収益率といった時系列データをもとにして、未来の値動きを予測したり、資産への投資がもたらすリスクを計測したりするFinancial Econometricsの分野で研究をしています。
私がよく扱うデータは、S&P500といった株価指数の収益率の時系列データです。例えば2022年10月12日と10月13日のS&P500の終値は2つの数字からなるベクトルで表され、それはデータ生成プロセス(Data Generating Process, DGP)から実現したものと考えます。もし世界の状況が違っていたら違う数字を要素に持つベクトルが実現したでしょうが、それはパラレルワールドに行くことができない限り観測することはできません。つまり時系列データは、DGPから実現したただ1つのベクトルだと言え、これがDGPからn個(標本サイズ)の実現値を得ることのできるi.i.d.(independent and identically distributed)データとの違いです。このような時系列データから有益な情報を得るには、DGPに仮定を置く必要があります。例えばある時点における収益率の期待値を時系列の平均によって推定するには、定常性を仮定する必要があります。この定常性が「過去の」時系列において正しいかどうかは、仮説検定によりある程度チェックすることはできますが、「未来の」時系列において正しいかどうかは、チェックする方法はありません。
私が主に興味を持っているのは、分析者が設定する仮定や時系列モデルが間違っていた場合の事です。その場合、予測やリスク計測といった分析結果にどのような影響が及ぶのか、より望ましい分析手法はないか、というテーマで研究しています。
より望ましい手法として、従来の分析で取られる「特定の1つの仮定が正しい」というスタンスを一歩弱めて、「特定の複数の仮定のうちどれかが正しい」というスタンスのもとで分析を行う「頑健性(Robustnes)」の考え方に着目し、金融分析に取り入れることを研究しています。それに関連して今関心を持っているのはオプション価格を用いた予測手法です。例えばヨーロピアン・オプションは、「将来のある時点に、ある資産(原資産)を、決められた価格(権利行使価格)で売る、または買うことができる権利」を指します。同じ原資産について複数の権利行使価格が用意されており、それぞれが市場で決まるオプション価格で取引されます。アセット・プライシングの理論を応用して、この権利行使価格とオプション価格の関係を原資産の予測に役立てる分析手法があります。権利行使価格の違いによるバラエティ豊かな情報を使い、オプションを売り買いする投資家が持つ見通しを引き出すという手法です。従来の時系列分析と違い定常性を仮定する必要がないなど優れた点が多くありますが、リスク中立確率(risk neutral distribution)という疑似的な確率のもとでの予測となってしまいます。リスク中立確率を現実の確率に変換する際に頑健性の考え方を導入する方法を提唱しています。
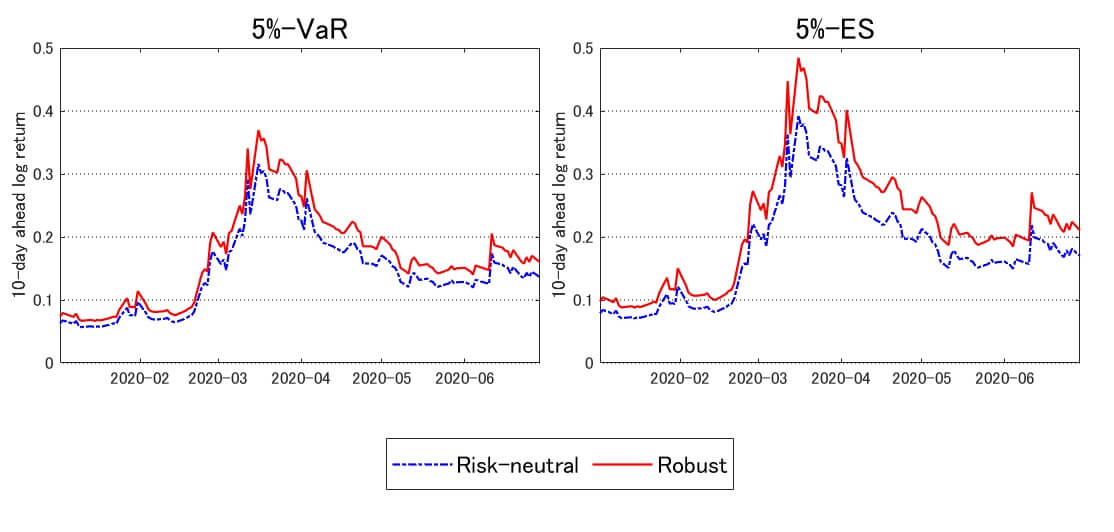
この図は、2つの主要なリスク指標であるバリューアットリスク(Value at Risk, VaR)と期待ショートフォール(Expected Shortfall, ES)を、オプション価格を用いて算出したものです。青色がリスク中立確率に基づく予測で、赤色が頑健性を用いて変換した確率に基づく予測になります。頑健性はより保守的なVaRとESを導く傾向があるため、赤色の線は常に青色より上回っています。これは、リスクをより大きく見積もっているという意味になります。
山下 真美子
YAMASHITA Mamiko
講師:Associate Professor
学位:Ph.D. in Economics(トゥールーズ第一大学)
yamashitam@osipp.osaka-u.ac.jp































