Field of Research

Financial Econometrics, Finance

Research Topics

Risk management, Forecasting

Overview of Research 

My research field is financial econometrics. I analyze the time series data of prices/returns of various assets traded in financial markets to forecast future prices/returns or measure the risk in an investment.

I mainly study the returns on the S&P500 index. For example, the closing price of the S&P500 on 10/12/2022 and 10/13/2022 can be expressed as a 2×1 vector, which is thought to be a realization of the Data Generating Process (DGP). If the state of the world were different, the realized vector would have been different; however, this “what if” situation can never be observed without traveling to a parallel world. In other words, the time-series data are the only realization of the DGP, which is the difference between independent and identically distributed (i.i.d.) data, in which there are n (i.e., the sample size) realizations of the DGP. Thus, assumptions are necessary to obtain useful information from the time-series data. For example, forecasts of the returns can be obtained by assuming that the stationarity holds for past and future returns. Although stationarity is testable based on previous series data, we will never know if it will still hold for the future.

I am particularly interested in cases in which these assumptions or the time-series models used in analyses are incorrect. If that is the case, to what extent are the results affected? Is there any method to incorporate possible misspecifications of the model into the analyses?

As an alternative approach, I consider the “robustness” in which an analyst believes one of the models they are considering is right. This is more flexible than the standard approach, which is based on the belief that one specific model is right. To apply this approach, I study option-implied forecasts. European options give the right to buy or sell an underlying asset at a fixed price (strike) at a fixed maturity date. Using the cross-section of the option prices with various strikes, it is possible to derive the investors’ outlook. Option-implied forecasts are therefore said to be forward-looking, and a stationarity assumption on the return process is not necessary. One challenge with this approach is that option prices only indicate risk-neutral distributions, artificial distributions different from the actual distribution. A transformation from risk-neutral to actual distributions is thus needed, and I try to introduce robustness theory into the transformation from risk-neutral to actual distributions.

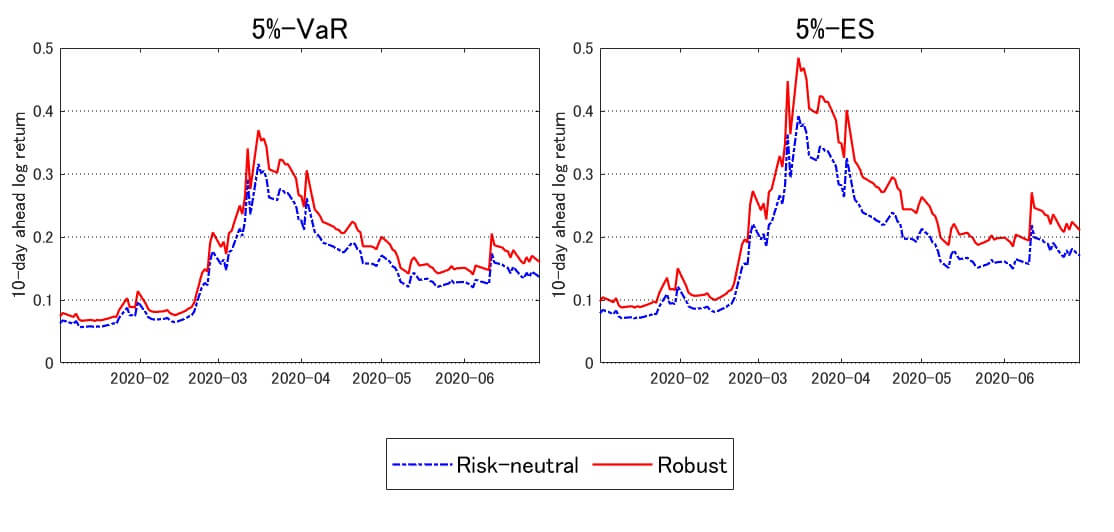
These figures demonstrate two commonly used risk measures, value-at-risk (VaR) and expected shortfall (ES), which are computed with option prices. The one based on the risk-neutral distribution is indicated in blue, and the one based on the robust transformation is in red. With VaR and ES, the robustness results in more conservative forecasts; that is, the risk is estimated to be larger.

YAMASHITA, Mamiko
Associate Professor
Degree: Ph.D. in Economics（Toulouse 1 Capitole University）
yamashitam@osipp.osaka-u.ac.jp